Code examples¶
Applications¶
Creep compliance analysis¶
This example uses the contour data of an cell in the OS to compute its GGF and creep compliance. The contour data were determined from this phase-contrast video (prior to video compression). During stretching, the total laser power was increased from 0.2W to 1.3W (reflexes due to second harmonic effects appear as white spots).
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 | import ggf
import h5py
import lmfit
import matplotlib.pylab as plt
import numpy as np
import percache
mycache = percache.Cache("creep_compliance.cache", livesync=True)
def ellipse_fit(radius, theta):
'''Fit a centered ellipse to data in polar coordinates
Parameters
----------
radius: 1d ndarray
radial coordinates
theta: 1d ndarray
angular coordinates [rad]
Returns
-------
a, b: floats
semi-axes of the ellipse; `a` is aligned with theta=0.
'''
def residuals(params, radius, theta):
a = params["a"].value
b = params["b"].value
r = a*b / np.sqrt(a**2 * np.sin(theta)**2 + b**2 * np.cos(theta)**2)
return r - radius
parms = lmfit.Parameters()
parms.add(name="a", value=radius.mean())
parms.add(name="b", value=radius.mean())
res = lmfit.minimize(residuals, parms, args=(radius, theta))
return res.params["a"].value, res.params["b"].value
@mycache
def get_ggf(**kw):
f = ggf.get_ggf(use_lut=True, **kw)
return f
# load the contour data (stored in polar coordinates)
with h5py.File("data/creep_compliance_data.h5", "r") as h5:
radius = h5["radius"].value * 1e-6 # [µm] to [m]
theta = h5["theta"].value
time = h5["time"].value
meta = dict(h5.attrs)
factors = np.zeros(len(radius), dtype=float)
semimaj = np.zeros(len(radius), dtype=float)
semimin = np.zeros(len(radius), dtype=float)
strains = np.zeros(len(radius), dtype=float)
complnc = np.zeros(len(radius), dtype=float)
for ii in range(len(radius)):
# determine semi-major and semi-minor axes
smaj, smin = ellipse_fit(radius[ii], theta[ii])
semimaj[ii] = smaj
semimin[ii] = smin
# compute GGF
print("compute ggf smaj={:.3e}, smin={:.3e}".format(smaj, smin))
if (time[ii] > meta["time_stretch_begin [s]"]
and time[ii] < meta["time_stretch_end [s]"]):
power_per_fiber=meta["power_per_fiber_stretch [W]"]
else:
power_per_fiber=meta["power_per_fiber_trap [W]"]
f = get_ggf(model="boyde2009",
semi_major=smaj,
semi_minor=smin,
object_index=meta["object_index"],
medium_index=meta["medium_index"],
effective_fiber_distance=meta["effective_fiber_distance [m]"],
mode_field_diameter=meta["mode_field_diameter [m]"],
power_per_fiber=power_per_fiber,
wavelength=meta["wavelength [m]"],
poisson_ratio=.5)
print("... ", ii, f)
factors[ii] = f
# compute compliance
strains = (semimaj-semimaj[0]) / semimaj[0]
complnc = strains / factors
compl_ival = (time>meta["time_stretch_begin [s]"]) * (time<meta["time_stretch_end [s]"])
stretch_index = np.where(compl_ival)[0][0]
complnc_1 = strains/factors[stretch_index]
# plots
plt.figure(figsize=(8, 7))
ax1 = plt.subplot(221, title="ellipse fit semi-axes")
ax1.plot(time, semimaj*1e6, label="semi-major axis")
ax1.plot(time, semimin*1e6, label="semi-minor axis")
ax1.legend()
ax1.set_xlabel("time [s]")
ax1.set_ylabel("axis radius [µm]")
ax2 = plt.subplot(222, title="GGF")
ax2.plot(time, factors)
ax2.set_xlabel("time [s]")
ax2.set_ylabel("global geometric factor [Pa]")
ax3 = plt.subplot(223, title="strain")
ax3.plot(time, (strains)*100)
ax3.set_xlabel("time [s]")
ax3.set_ylabel("deformation $w(t)/r_0$ [%]")
ax4 = plt.subplot(224, title="compliance")
ax4.plot(time[compl_ival], complnc_1[compl_ival], label="single GGF")
ax4.plot(time[compl_ival], complnc[compl_ival], label="series GGF")
ax4.legend()
ax4.set_xlabel("time [s]")
ax4.set_ylabel("creep compliance $J(t)$ [Pa⁻¹]")
for ax in [ax1, ax2, ax3, ax4]:
ax.set_xlim(0, np.round(time.max()))
ax.axvline(x=meta["time_stretch_begin [s]"], c="r")
ax.axvline(x=meta["time_stretch_end [s]"], c="r")
plt.tight_layout()
plt.show()
|
Reproduction tests¶
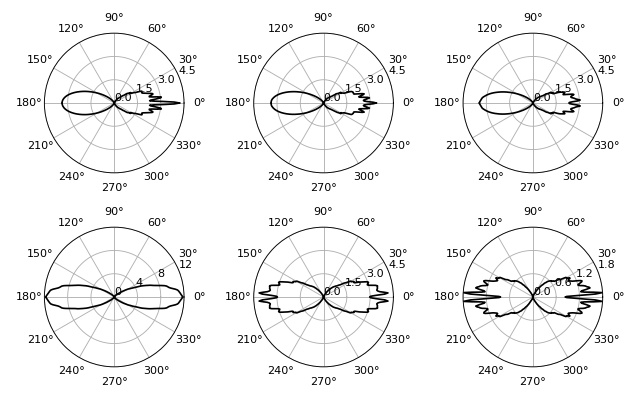
Radial stresses of a prolate spheroid¶
This examples computes radial stress profiles for spheroidal objects in the optical stretcher, reproducing figures (9) and (10) of [BCG09].
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 | import matplotlib.pylab as plt
import numpy as np
import percache
from ggf.stress.boyde2009.core import stress
@percache.Cache("stress_reproduced.cache", livesync=True)
def compute(**kwargs):
"Locally cached version of ggf.core.stress"
return stress(**kwargs)
# variables from the publication
alpha = 47
wavelength = 1064e-9
radius = alpha * wavelength / (2 * np.pi)
kwargs = {"stretch_ratio": .1,
"object_index": 1.375,
"medium_index": 1.335,
"wavelength": wavelength,
"beam_waist": 3,
"radius": radius,
"power_left": 1,
"power_right": 1,
"poisson_ratio": 0,
"n_points": 200,
}
kwargs1 = kwargs.copy()
kwargs1["power_right"] = 0
kwargs1["stretch_ratio"] = 0
kwargs1["dist"] = 90e-6
kwargs2 = kwargs.copy()
kwargs2["power_right"] = 0
kwargs2["stretch_ratio"] = .05
kwargs2["dist"] = 90e-6
kwargs3 = kwargs.copy()
kwargs3["power_right"] = 0
kwargs3["stretch_ratio"] = .1
kwargs3["dist"] = 90e-6
kwargs4 = kwargs.copy()
kwargs4["dist"] = 60e-6
kwargs5 = kwargs.copy()
kwargs5["dist"] = 120e-6
kwargs6 = kwargs.copy()
kwargs6["dist"] = 200e-6
# polar plots
plt.figure(figsize=(8, 5))
th1, sigma1 = compute(**kwargs1)
ax1 = plt.subplot(231, projection='polar')
ax1.plot(th1, sigma1, "k")
ax1.plot(th1 + np.pi, sigma1[::-1], "k")
th2, sigma2 = compute(**kwargs2)
ax2 = plt.subplot(232, projection='polar')
ax2.plot(th2, sigma2, "k")
ax2.plot(th2 + np.pi, sigma2[::-1], "k")
th3, sigma3 = compute(**kwargs3)
ax3 = plt.subplot(233, projection='polar')
ax3.plot(th3, sigma3, "k")
ax3.plot(th3 + np.pi, sigma3[::-1], "k")
for ax in [ax1, ax2, ax3]:
ax.set_rticks([0, 1.5, 3, 4.5])
ax.set_rlim(0, 4.5)
th4, sigma4 = compute(**kwargs4)
ax4 = plt.subplot(234, projection='polar')
ax4.plot(th4, sigma4, "k")
ax4.plot(th4 + np.pi, sigma4[::-1], "k")
ax4.set_rticks([0, 4, 8, 12])
ax4.set_rlim(0, 12)
th5, sigma5 = compute(**kwargs5)
ax5 = plt.subplot(235, projection='polar')
ax5.plot(th5, sigma5, "k")
ax5.plot(th5 + np.pi, sigma5[::-1], "k")
ax5.set_rticks([0, 1.5, 3, 4.5])
ax5.set_rlim(0, 4.5)
th6, sigma6 = compute(**kwargs6)
ax6 = plt.subplot(236, projection='polar')
ax6.plot(th6, sigma6, "k")
ax6.plot(th6 + np.pi, sigma6[::-1], "k")
ax6.set_rticks([0, 0.6, 1.2, 1.8])
ax6.set_rlim(0, 1.8)
for ax in [ax1, ax2, ax3, ax4, ax5, ax6]:
ax.set_thetagrids(np.linspace(0, 360, 12, endpoint=False))
plt.tight_layout()
plt.show()
|
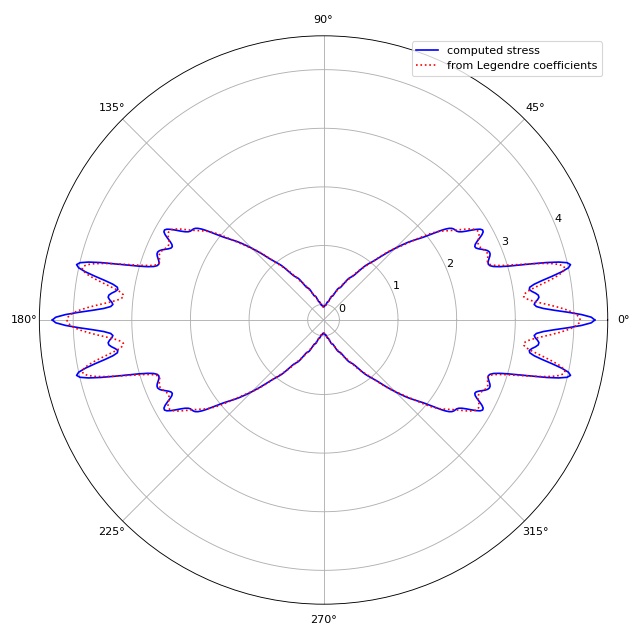
Decomposition of stress in Legendre polynomials¶
To compute the GGF, ggf.globgeomfact.coeff2ggf() uses the
coefficients of the decomposition of the stress into Legendre
polynomials \(P_n(\text{cos}(\theta))\). This example visualizes
the small differences between the original stress and the stress
computed from the Legendre coefficients. This plot is automatically
produced by the original Matlab script StretcherNStress.m.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 | import matplotlib.pylab as plt
import numpy as np
import percache
from ggf.sci_funcs import legendrePlm
from ggf.stress.boyde2009.core import stress
@percache.Cache("stress_decomposition.cache", livesync=True)
def compute(**kwargs):
"Locally cached version of ggf.core.stress"
return stress(**kwargs)
# compute default stress
theta, sigmarr, coeff = compute(ret_legendre_decomp=True,
numpoints=300)
# compute stress from coefficients
numpoints = theta.size
sigmarr_c = np.zeros((numpoints, 1), dtype=float)
for ii in range(numpoints):
for jj, cc in enumerate(coeff):
sigmarr_c[ii] += coeff[jj] * \
np.real_if_close(legendrePlm(0, jj, np.cos(theta[ii])))
# polar plot
plt.figure(figsize=(8, 8))
ax = plt.subplot(111, projection="polar")
plt.plot(theta, sigmarr, '-b', label="computed stress")
plt.plot(theta + np.pi, sigmarr[::-1], '-b')
plt.plot(theta, sigmarr_c, ':r', label="from Legendre coefficients")
plt.plot(theta + np.pi, sigmarr_c[::-1], ':r')
plt.legend()
plt.tight_layout()
plt.show()
|
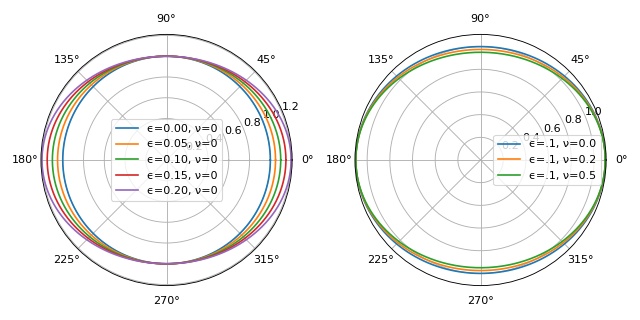
Object boundary: stretching and Poisson’s ratio¶
This example illustrates how the parameters Poisson’s ratio
\(\nu\) and stretch ratio \(\epsilon\) influence
the object boundary used in ggf.core.stress() and
defined in ggf.core.boundary().
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 | import numpy as np
import matplotlib.pylab as plt
from ggf.stress.boyde2009 import boundary
theta = np.linspace(0, 2*np.pi, 300)
costheta = np.cos(theta)
# change epsilon
eps = [.0, .05, .10, .15, .20]
b1s = []
for ep in eps:
b1s.append(boundary(costheta=costheta,
epsilon=ep,
nu=.0))
# change Poisson's ratio
nus = [.0, .25, .5]
b2s = []
for nu in nus:
b2s.append(boundary(costheta=costheta,
epsilon=.1,
nu=nu))
# plot
plt.figure(figsize=(8, 4))
ax1 = plt.subplot(121, projection="polar")
for ep, bi in zip(eps, b1s):
ax1.plot(theta, bi, label="ϵ={:.2f}, ν=0".format(ep))
ax1.legend()
ax2 = plt.subplot(122, projection="polar")
for nu, bi in zip(nus, b2s):
ax2.plot(theta, bi, label="ϵ=.1, ν={:.1f}".format(nu))
ax2.legend()
plt.tight_layout()
plt.show()
|